四角形の面積公式 $$正方形=1辺\times 1辺$$ $$長方形=たて\times よこ$$ $$平行四辺形=底辺\times 高さ$$ $$ひし形=対角線\times 対角線\times \frac{1}{2}$$ $$台形=(上底下底)\times 高さ\times \frac{1}{2}$$ 〇 底面積は四角形の種類によって、面積の公式を使い分けてね!次は小数点を含む平行四辺形の面積を計算します。 練習問題② 底辺が 28(cm)、高さが 46(cm)の平行四辺形の面積を求めてみましょう。 平行四辺形の面積を求める公式は 平行四辺形の面積 \(=\) 底辺 \(\times\) 高さ なので、平行四辺形の面積を \(S\) とすると・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。
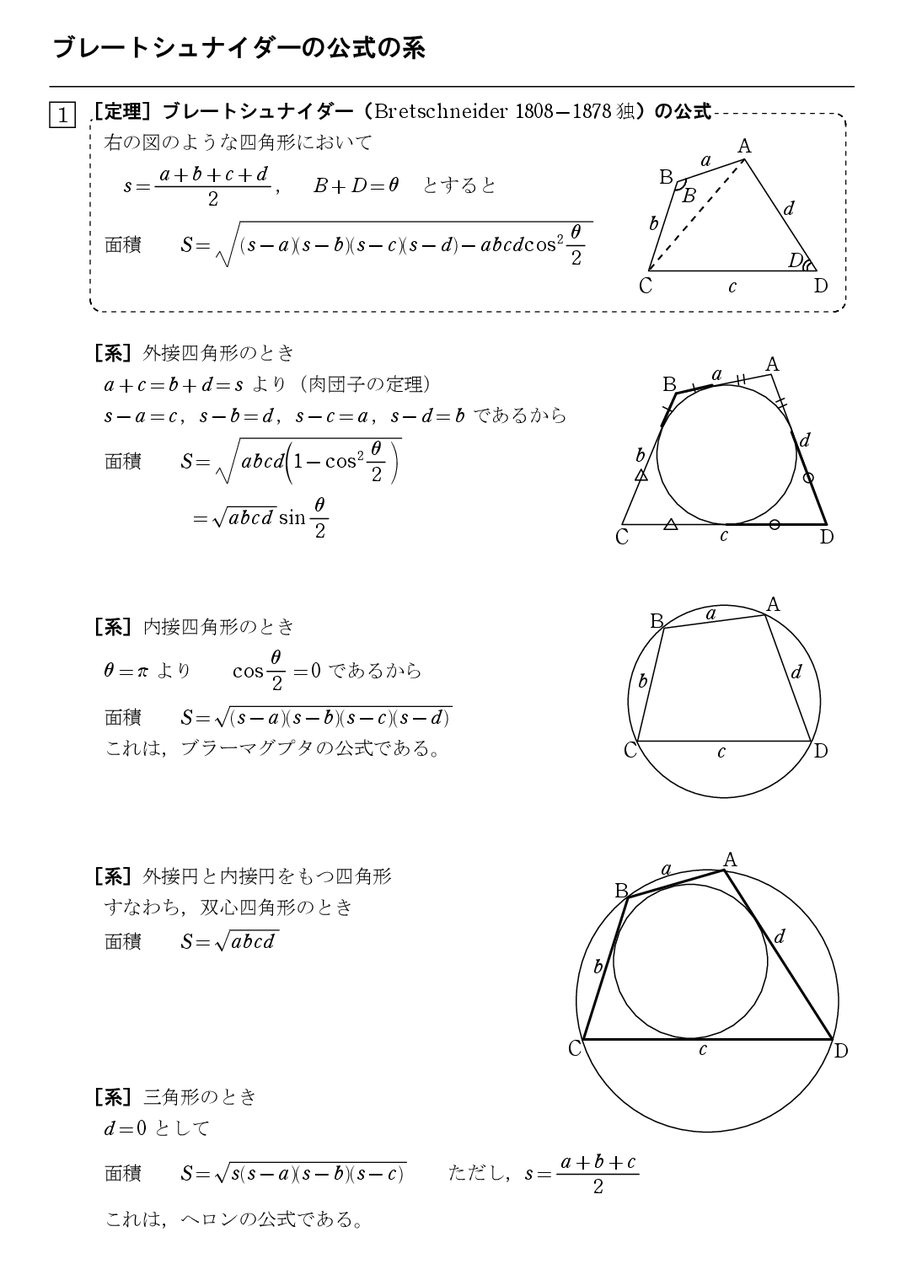
対角線から四角形の面積を求める公式を1分で証明する 怜悧玲瓏 高校数学を天空から俯瞰する
四角形 の 面積 の 公式
四角形 の 面積 の 公式-形や四角形の面積を求めることができる。 知 必要な部分の長さを測ることによって,既習・ 高さや底辺の意味を理解し,三角形や四 理の公式を使い,三角形や四角形の面積が求めら 角形の向きや形にかかわらず公式を使って形についても形を四角形に変形させて公式を用いれば面積が求められることを学習させたい。また、1 平方センチメートルと1 平方メートルの実際の広さを視覚化して、量感を育てていきたい。 3 単元計画 *研究内容(2)評価問題を位置付けた指導過程



19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
4点の座標から面積 4点の座標から四角形の面積を計算する方法の考え方を知りたいと思います。 測量では三斜法と言うようです。どうやら、この方法は、三角形以上の凸多角形の面積が計算できそうです。 4点 a,b,c,d が上の図のような配置だとします。次は小数点を含む平行四辺形の面積を計算します。 練習問題② 底辺が 28(cm)、高さが 46(cm)の平行四辺形の面積を求めてみましょう。 平行四辺形の面積を求める公式は 平行四辺形の面積 \(=\) 底辺 \(\times\) 高さ なので、平行四辺形の面積を \(S\) とすると証明 四角形の面積を S とすると、 = より = を得る。また、余弦定理より、 = − = − であるから ( − −) = −を得る。4S 2 についての式と辺々を足し合わせ、加法定理 cos(A C) = cos A cos C − sin A sin C を用いると、 ( − −) = − () となる。倍角の公式 = を用いて変形すると、
四角形の面積の求め方(公式) 三角形に分けて面積を求める s:台形までの面積の公式はわかったけど、台形でない四角形の体積を求める公式はあるんですか? T:左の図のような四角形の面積をどうやって求めたらいいのか、ということですね。 s:そう四角形 4角形 面積計算 公式 求め方 正方形 長方形 縦 横 自動 area1.単元名 四角形と三角形の面積(台形の面積) 2.題材について (1)題材のねらい 本題材は、小学校学習指導要領 算数における第5学年の内容b(1) を基に構成されている。 B「量と測定」(1)図形の面積を計算によって求めることができるようにする
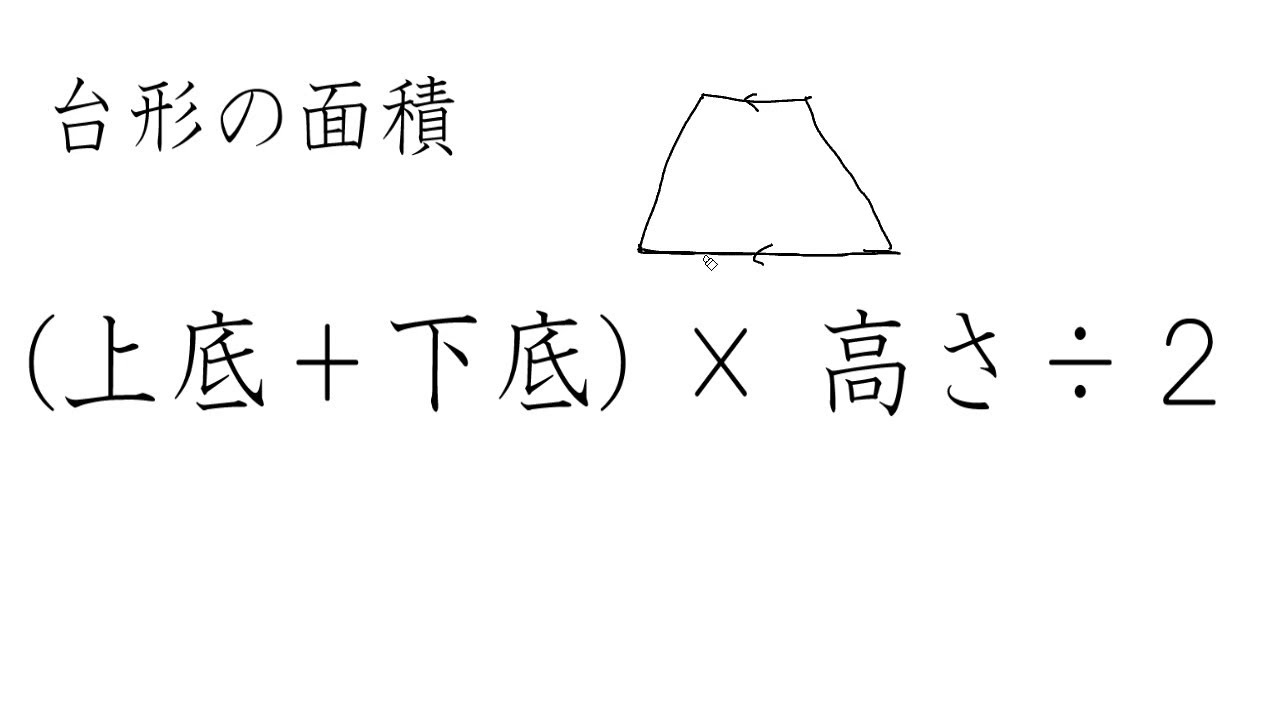
四角形の面積を求める公式は、どれも三角形の面積を求める公式から得ることが出来ます。四角形に 対角線 (たいかくせん) を引くと、三角形に分けられますよね?平行四辺形の面積を求める公式を書きましょう。 三角形の面積を求める公式を書きましょう。 次の図形の面積を求めましょう。 ① ② 6×3=18 8×5=40 ③ ④ 12×7÷2=42 4×7÷2=14 6㎝ 3㎝ 12㎝ 7㎝ 基本の確かめ 平行四辺形の面積 = 底辺 × 高さ 三角形の面積台形の面積の求め方を既 習の形を作り出すアイディ アで多様に考え説明すると ともに、簡便さからその考え をまとめる。 台形の求積公式「(上底+ 下底)×高さ÷2」の意味を理 解 する。 ⑬⑭⑮ 面積の求積のまとめ 一般四角形や多角形の 面積を三角形
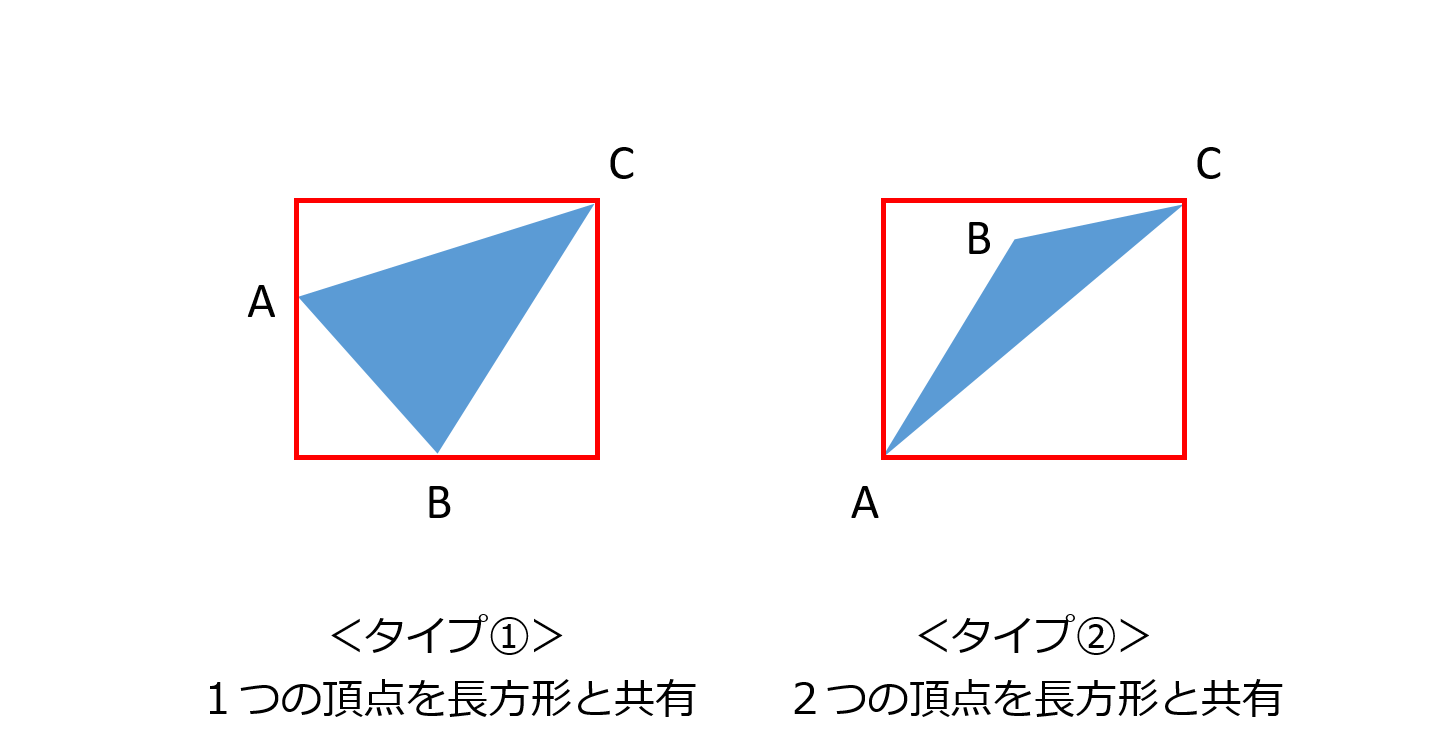


正方形の中にある三角形の面積の平均の求め方 三角形を分解して組み立てなおす Musyokutoumei


2
正三角形の面積 三角形の面積(底辺と高さから) 三角形の面積(2辺と夾角から) 三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから)四角形の面積の計算順を守るべき理由 小学校で四角形の面積の求め方は「縦*横」と習います。 そして当然ですがこの計算結果は、順序を「横*縦」に逆転させても同じになります。 縦3cm横5cmの長方形だった場合、以下のようになります。 縦×横:3 * 5 = 15形の面積の公式を考え、説明 している。 技平行四辺形の面積の公式を用 いて面積を求めることがで きる。 3 高さが平行四辺形の外に ある場合でも、平行四辺 形の面積の公式を適用で きることを理解する。 ・高さが平行四辺形の外にある場合の面


Edu City Chigasaki Kanagawa Jp Res Projects School Page 002 001 800 2ndmath Pdf


5年 平行四辺形の面積 算数イメージ動画集 大日本図書
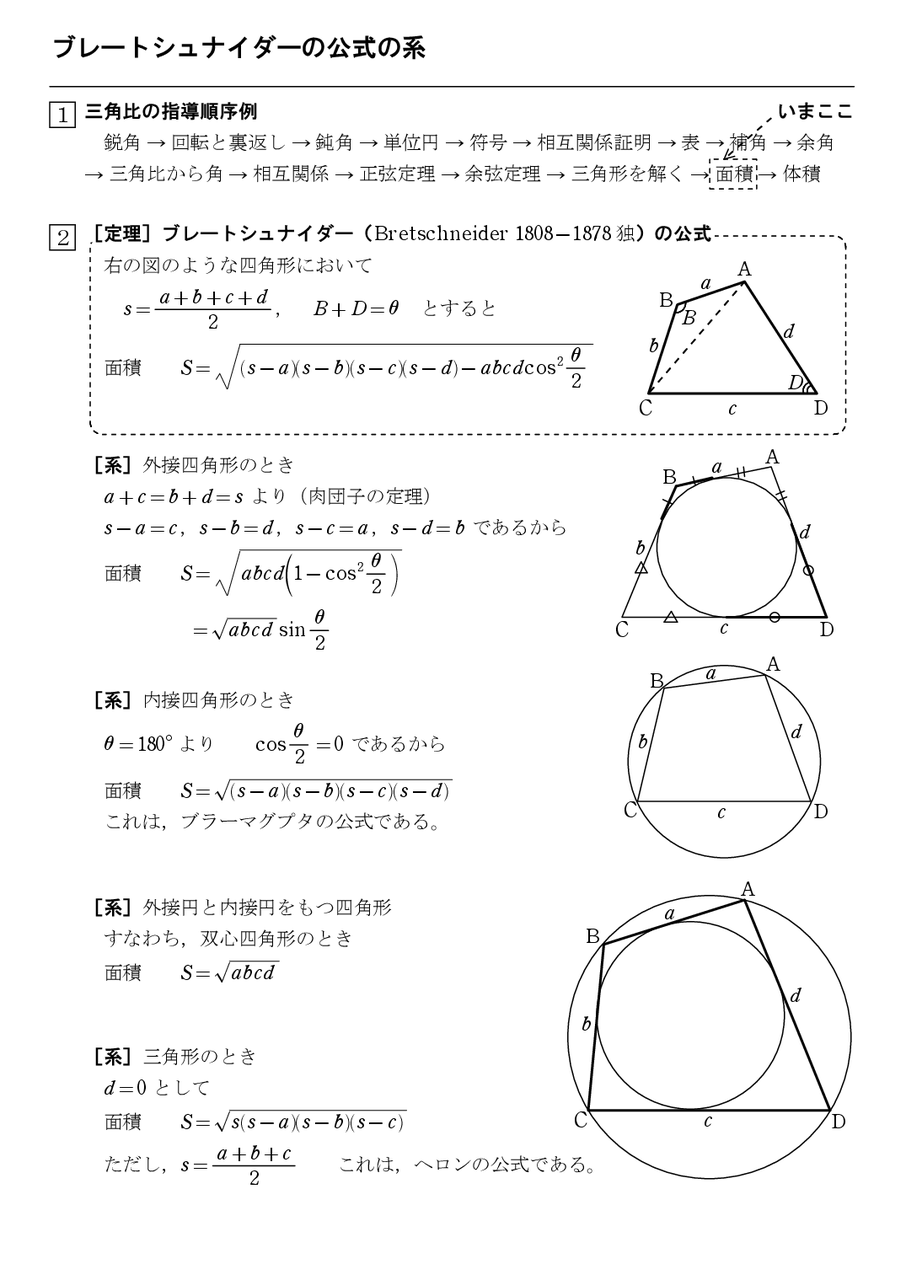
・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。5年 面積 子どもの学習支援 by いっちに算数 スマホ版 ① 三角形と平行四辺形と台形・ひし形の面積の求め方 ② 三角形と平行四辺形と台形・ひし形の面積求め方の公式 ③ いろいろな三角形・四角形の面積の求め方概要 ブラーマグプタの公式は、7世紀にインドの数学者 ブラーマグプタがヘロンの公式の一般化として得た定理である。 ヘロンの公式は三角形の3辺の長さから三角形の面積を求める公式であるが、ブラーマグプタの公式は四角形の 4辺の長さから四角形の面積を求める公式である。
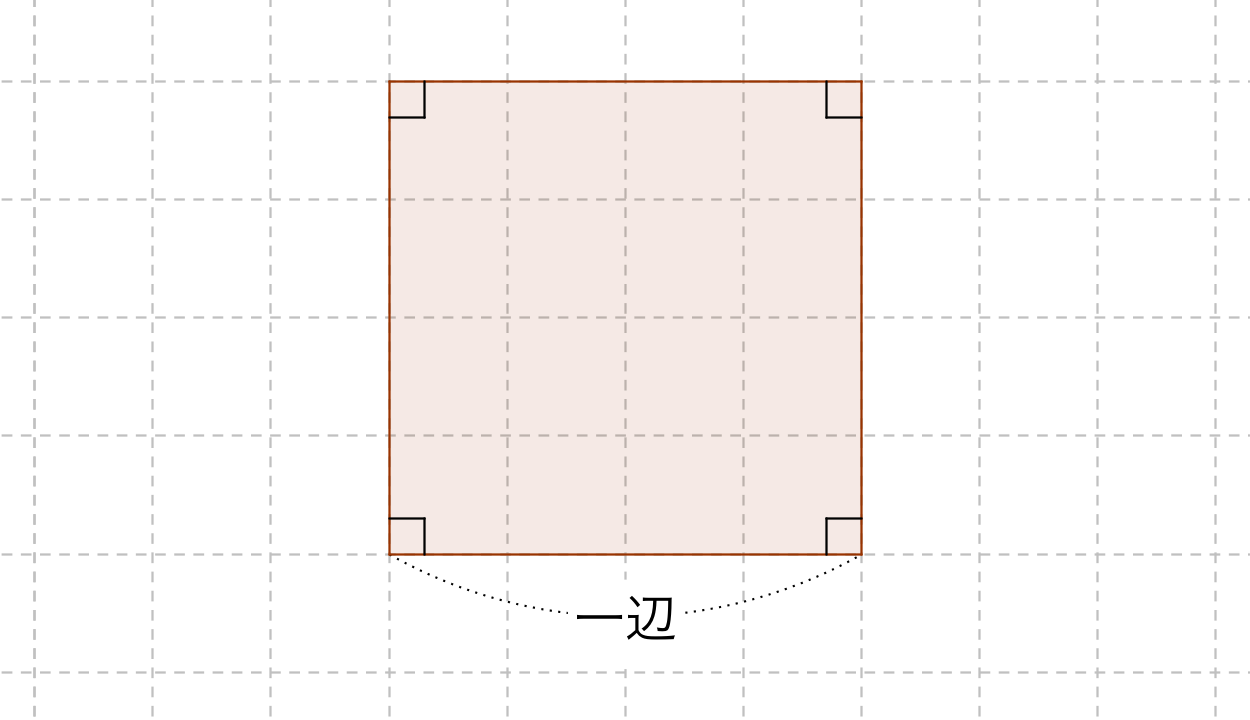


正方形の面積の公式 算数の公式
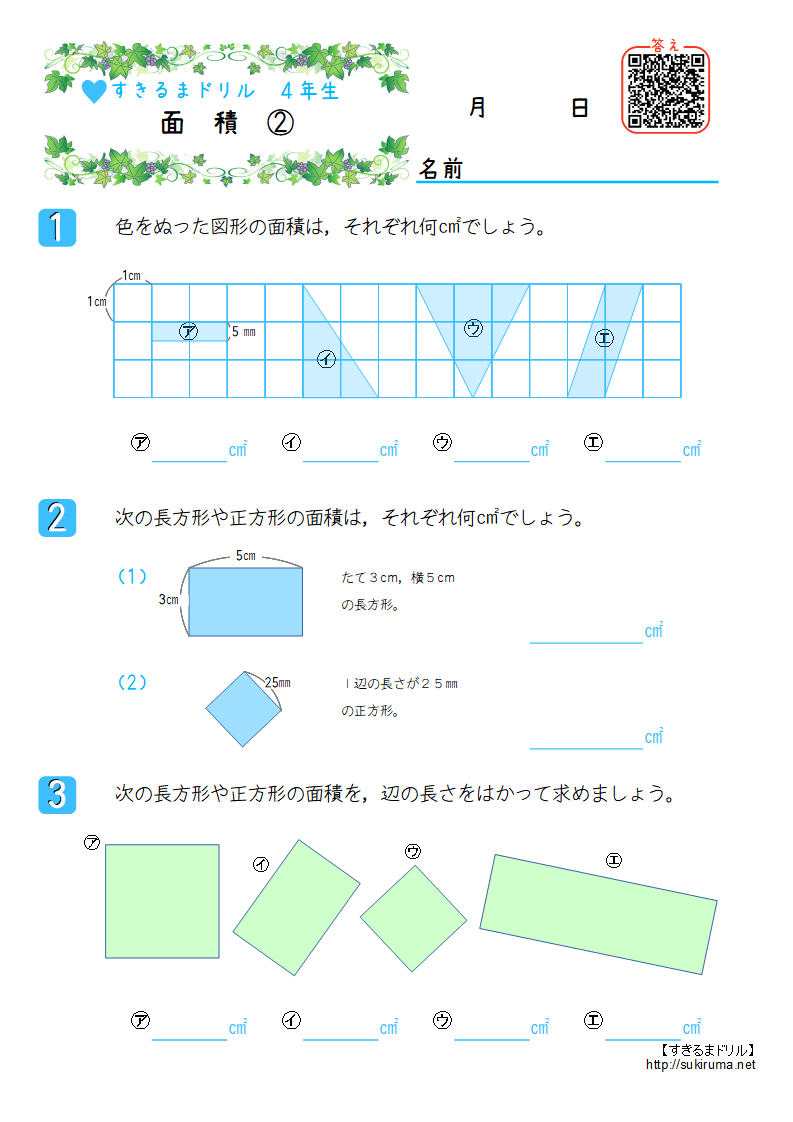


すきるまドリル 小学4年生 算数 面積 無料学習プリント すきるまドリル 無料学習プリント
形についても形を四角形に変形させて公式を用いれば面積が求められることを学習させたい。また、1 平方センチメートルと1 平方メートルの実際の広さを視覚化して、量感を育てていきたい。 3 単元計画 *研究内容(2)評価問題を位置付けた指導過程て,三角形の面積の公式を考 え,説明している。 技平行四辺形の面積の公式を 用いて面積を求めることが できる。 6 高さが三角形の外に ある場合でも,三角 形の面積の公式が適 用できることを理解 する。 どんな形の三角形で も,底辺の長さと高四角形の面積の計算順を守るべき理由 小学校で四角形の面積の求め方は「縦*横」と習います。 そして当然ですがこの計算結果は、順序を「横*縦」に逆転させても同じになります。 縦3cm横5cmの長方形だった場合、以下のようになります。 縦×横:3 * 5 = 15
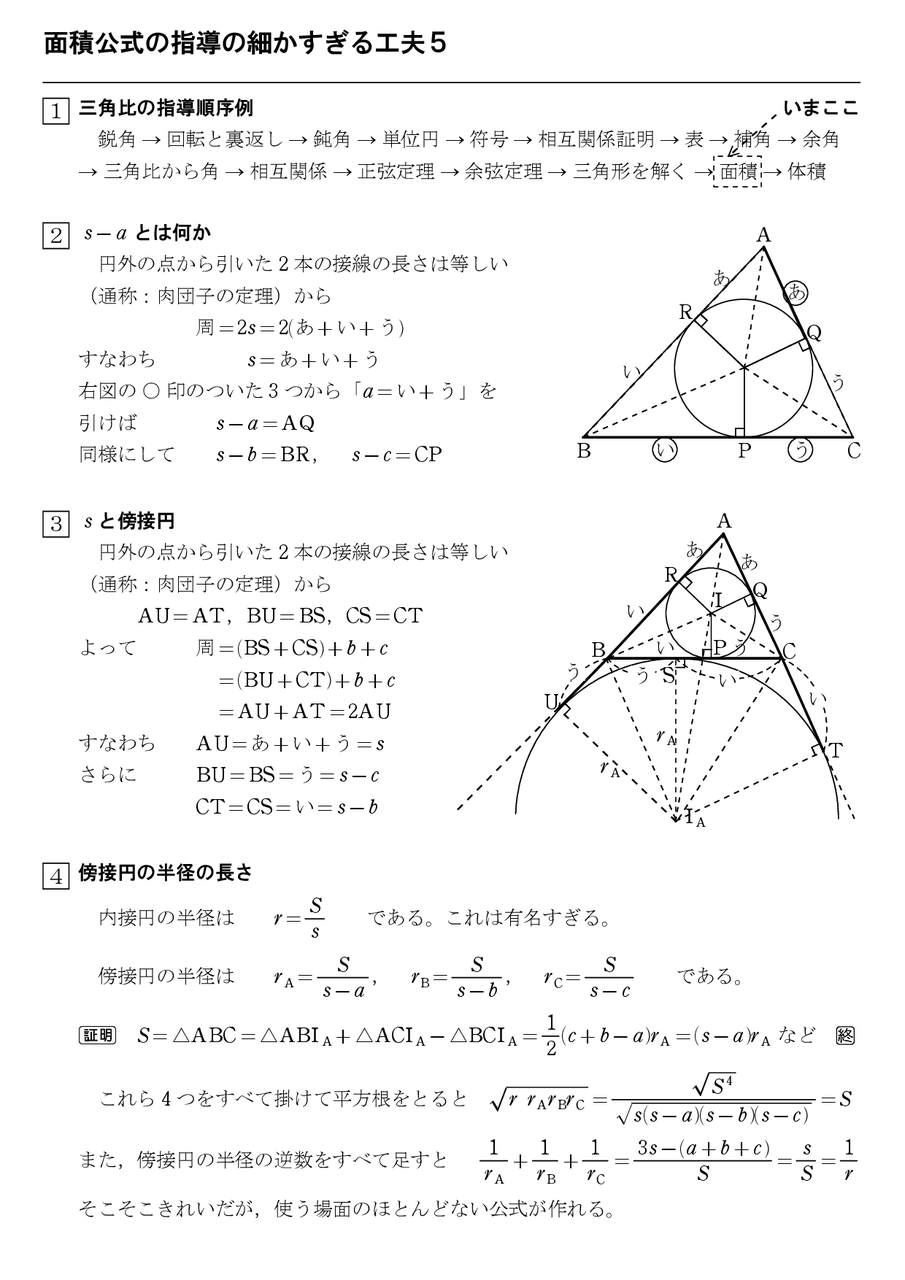


円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する



三角形の面積の公式 算数の公式
三角形の面積 3辺の長さがa,b,cの三角形の面積を求めるには、Aから辺BCへ垂線をたらし、その足をHとしてAH=hとおきます。 ABCの面積は ですが、ahをa,b,cだけの式に直すと、ヘロンの公式となります。四角形abcdの面積は 8+75=155㎠ よって、 答え 155㎠ 例題6 下の図のような台形abcdがあります。点pは、頂点aより出発して台形abcdの辺上を秒速2cmの速さで、頂点b、頂点c、を通って頂点dまで進みます。11秒後の四角形abcpの面積を求めなさい。 解説三角形の面積比にまつわる公式たち 中学数学チックな公式です。チェバの定理の証明に応用したり三次元に拡張したり。 複素数平面における三角形の面積 三角形の面積を求める公式の複素数平面バージョンです。 四角形の面積にまつわる公式 ブラーマ



四角形 Wikipedia


Www Shinko Keirin Co Jp Keirinkan Tea Sho Keyproject Pdf Sansu 5nen2 02 Pdf
正三角形の面積 三角形の面積(底辺と高さから) 三角形の面積(2辺と夾角から) 三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから)はじめに ここでは、ベクトルを用いた三角形の面積の求め方、その公式について説明しています。 面積を求める公式 図のように、 と で張られる三角形の面積をSとします。 このとき、面積Sは、次のように表すことができます。 これを四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。
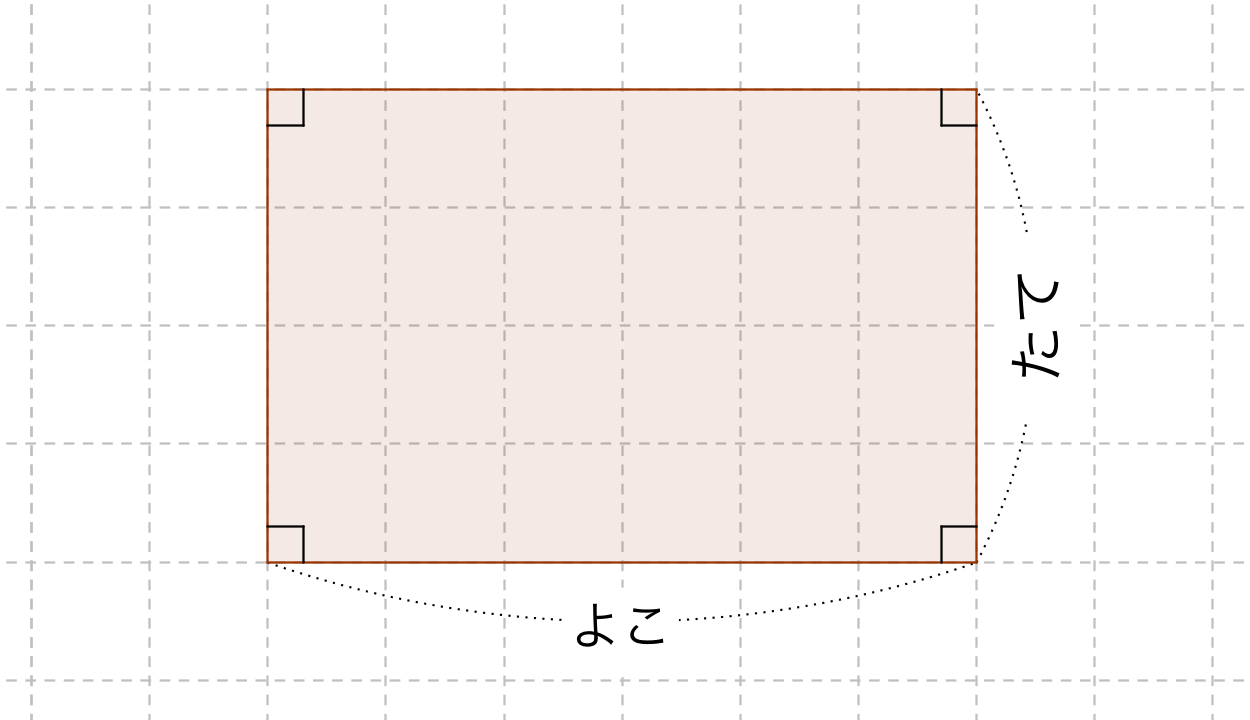


長方形の面積の公式 算数の公式


Www Wakayama Wky Ed Jp Nagusa Wp Content Uploads Sites 52 18 03 Afa4f4ae2913a9c5643adc5 1 Pdf
四角形abcdの面積は 8+75=155㎠ よって、 答え 155㎠ 例題6 下の図のような台形abcdがあります。点pは、頂点aより出発して台形abcdの辺上を秒速2cmの速さで、頂点b、頂点c、を通って頂点dまで進みます。11秒後の四角形abcpの面積を求めなさい。 解説四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。四角形の面積公式 $$正方形=1辺\times 1辺$$ $$長方形=たて\times よこ$$ $$平行四辺形=底辺\times 高さ$$ $$ひし形=対角線\times 対角線\times \frac{1}{2}$$ $$台形=(上底下底)\times 高さ\times \frac{1}{2}$$ 〇 底面積は四角形の種類によって、面積の公式を使い分けてね!
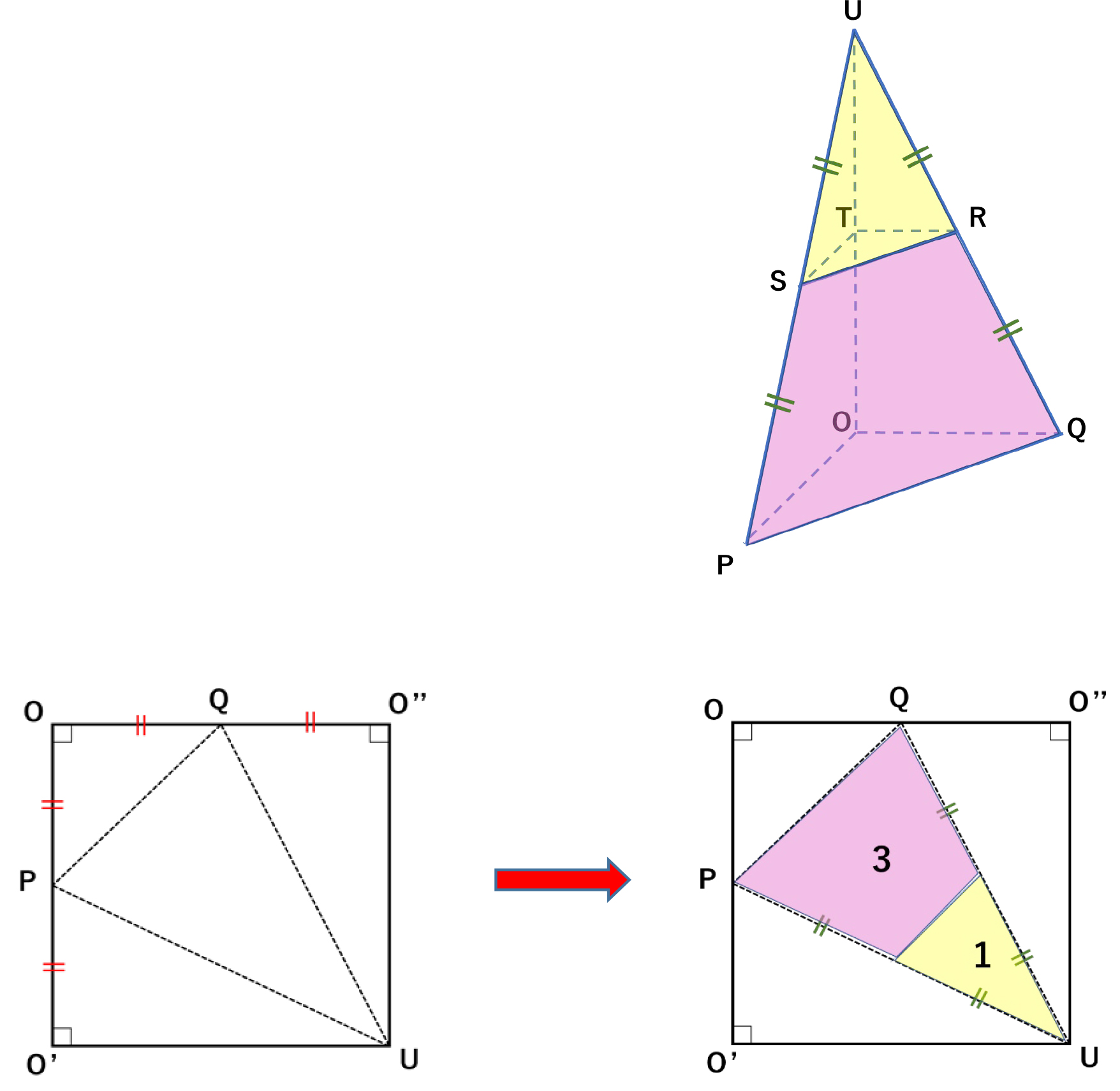


よく見かけますね この展開図 後編 中学受験プロ講師ブログ


Http Sanssouci Sakura Ne Jp Pdf Ta Menseki Pdf
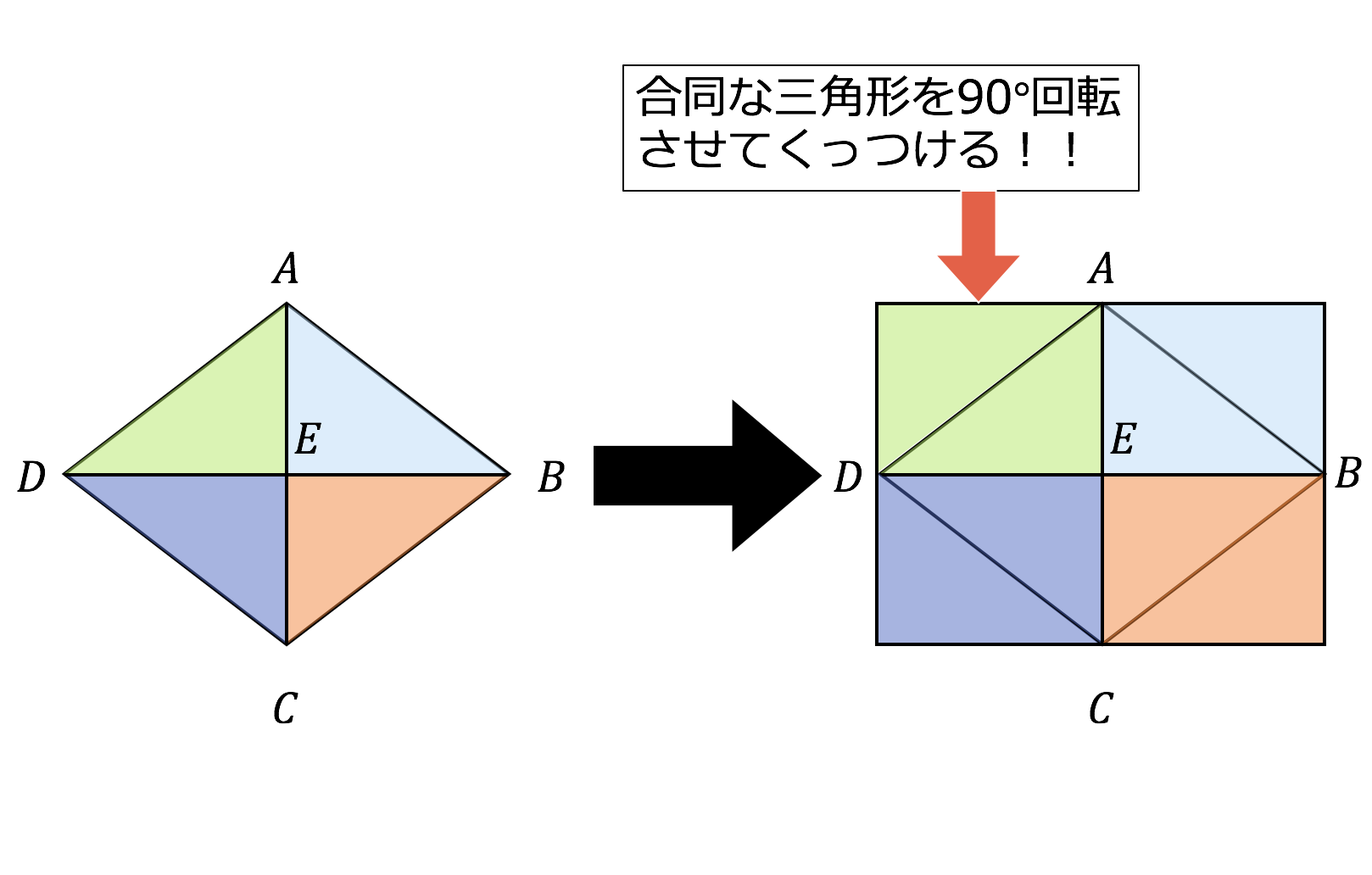


3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ


Www Wakayama Wky Ed Jp Nagusa Wp Content Uploads Sites 52 16 01 86b6728cf9efb1f9d16fe2c0d01 Pdf


Www Junten Ed Jp Contents Wp Content Uploads 13 04 90f3dca3ecefd1db Pdf



図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



ベストセレクション 対角線が垂直に交わる四角形の面積 デザイン文具
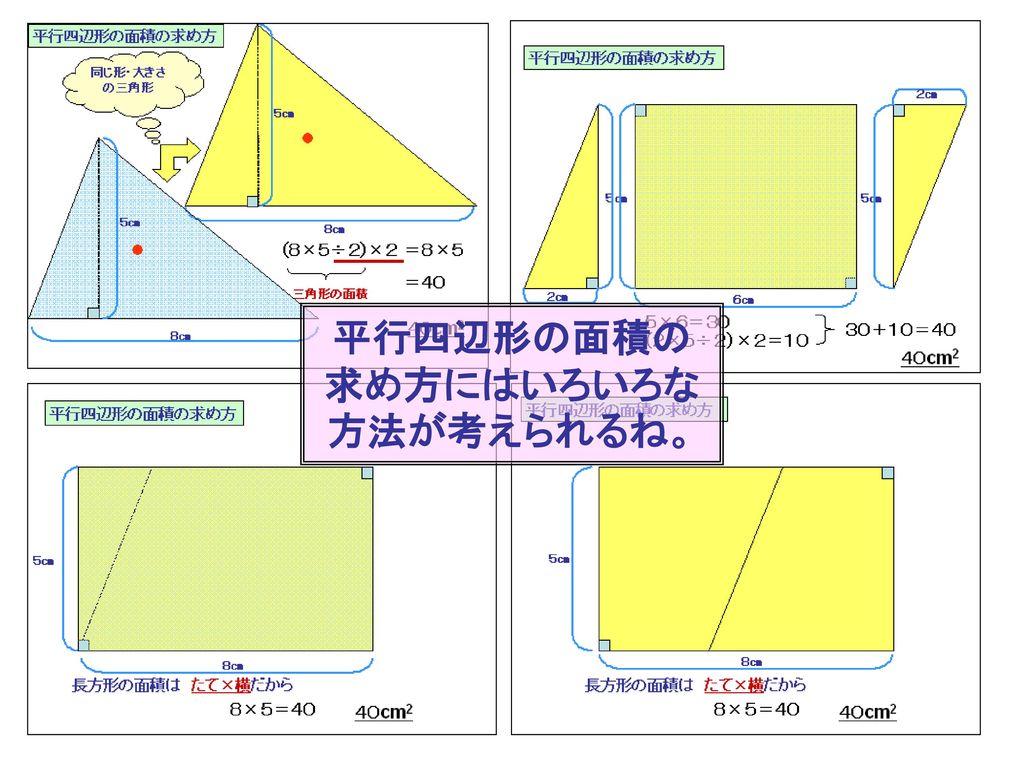


5年 面積 Ppt Download
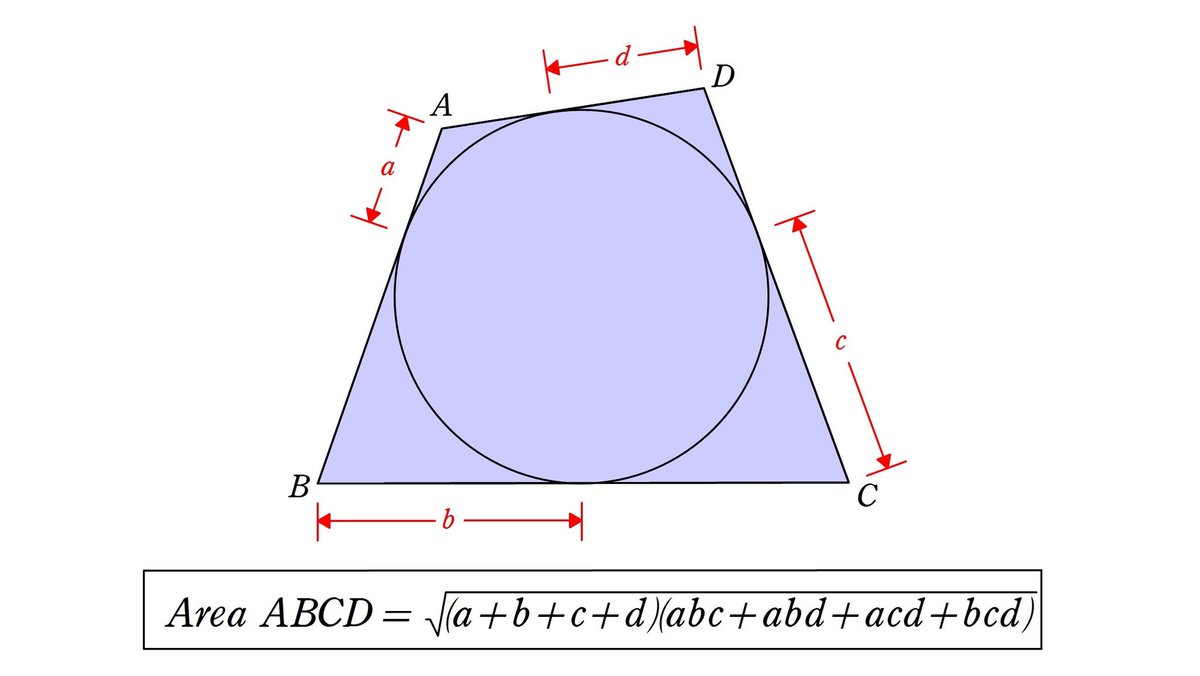


ポテト一郎 円に外接する四角形の面積 なんと 角の大きさに依存しません



高校数学テクニック集 002 数学 A 三角比 四角形の面積を求める公式 大学受験対策 数学i 図形と計量 学習塾 Dear Hope ディアホープ 改訂 Youtube


Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf



高校数学 円に内接する四角形の対角線の長さと面積 受験の月



膨四角形っていうものとか 小沢志朗江戸日記



高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月



長方形の面積の公式 算数の公式


図形の面積 算数 指導案 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート


Http Www Keirinkan Wakuwaku Com Kaitou Pdf 5 Second Volume Pdf
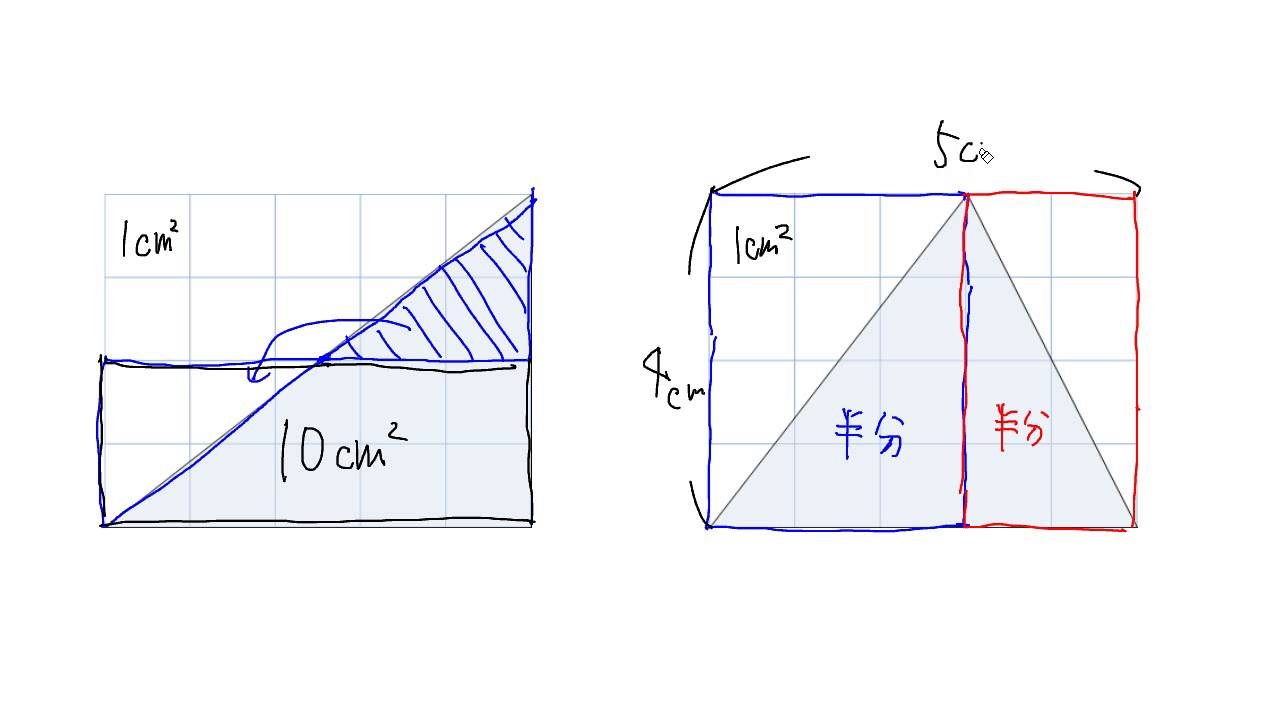


三角形 四角形の面積 Ict教材eboard イーボード
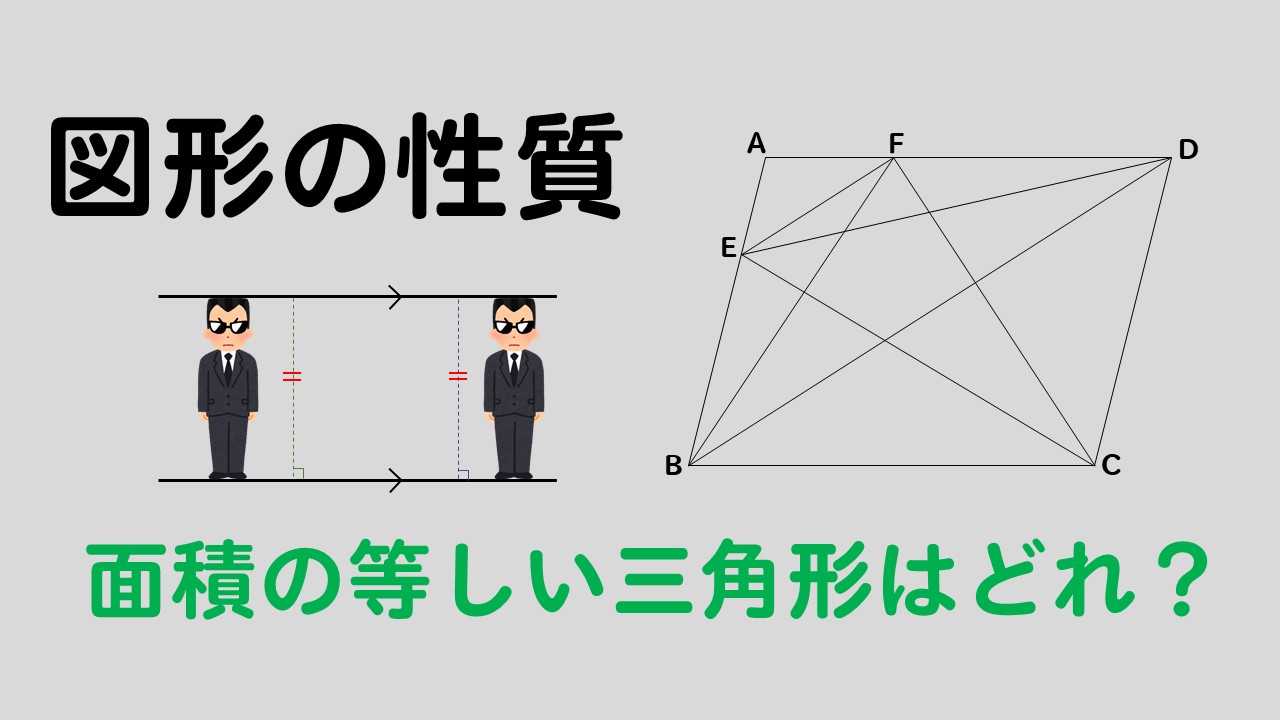


中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ



どのように式を立てればよいですか Clear



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月


Http Www Ota Ed Jp Josai Gakuryokukouzyou 10 sidouann4 Pdf


Http Masudahp Web Fc2 Com Kosu Pdf 111menseki1 Pdf



簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく


Http Www Suginami School Ed Jp Shinomiyashou 5 3kai Pdf


Http Www1 Center Spec Ed Jp Index Php Action Multidatabase Action Main Filedownload Download Flag 1 Upload Id 7861 Metadata Id W 640 Nc Session 90nprnk0a7nh47nmgakrigp1



ブレートシュナイダーの公式 Wikipedia


2



一般の四角形の面積 ブレートシュナイダーの公式 怜悧玲瓏 高校数学を天空から俯瞰する



円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する
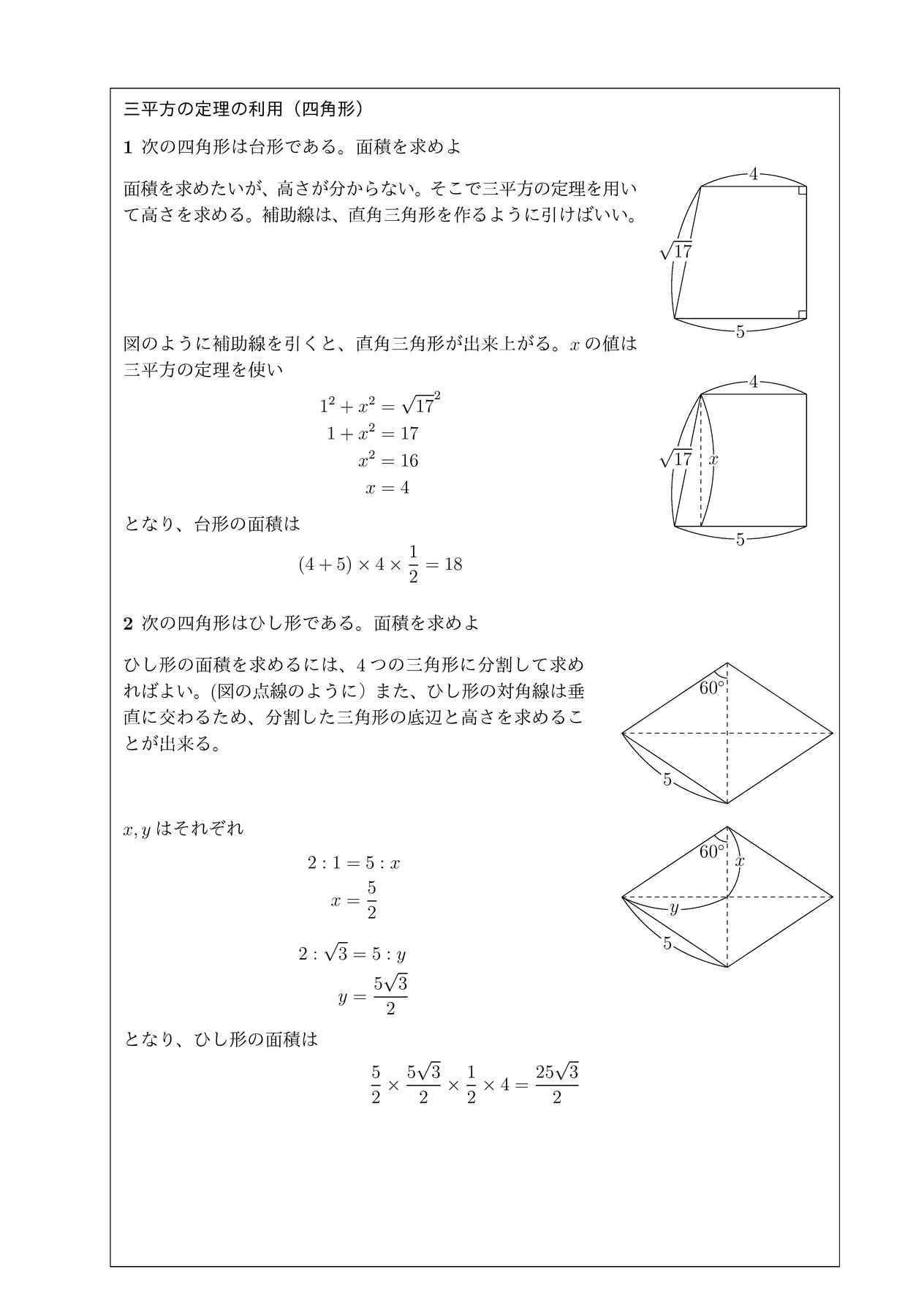


三平方の定理の利用 四角形 チーム エン



ベストセレクション 対角線が垂直に交わる四角形の面積 デザイン文具



対角線から四角形の面積を求める公式を1分で証明する 怜悧玲瓏 高校数学を天空から俯瞰する



対角線から四角形の面積を求める公式を1分で証明する 怜悧玲瓏 高校数学を天空から俯瞰する



三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



正方形 Wikipedia


Www Edu City Yokohama Jp Sch Kenkyu Es Ict Kukennhodogayasannsuu14 Pdf



ブラーマグプタの公式 東大合格コム



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
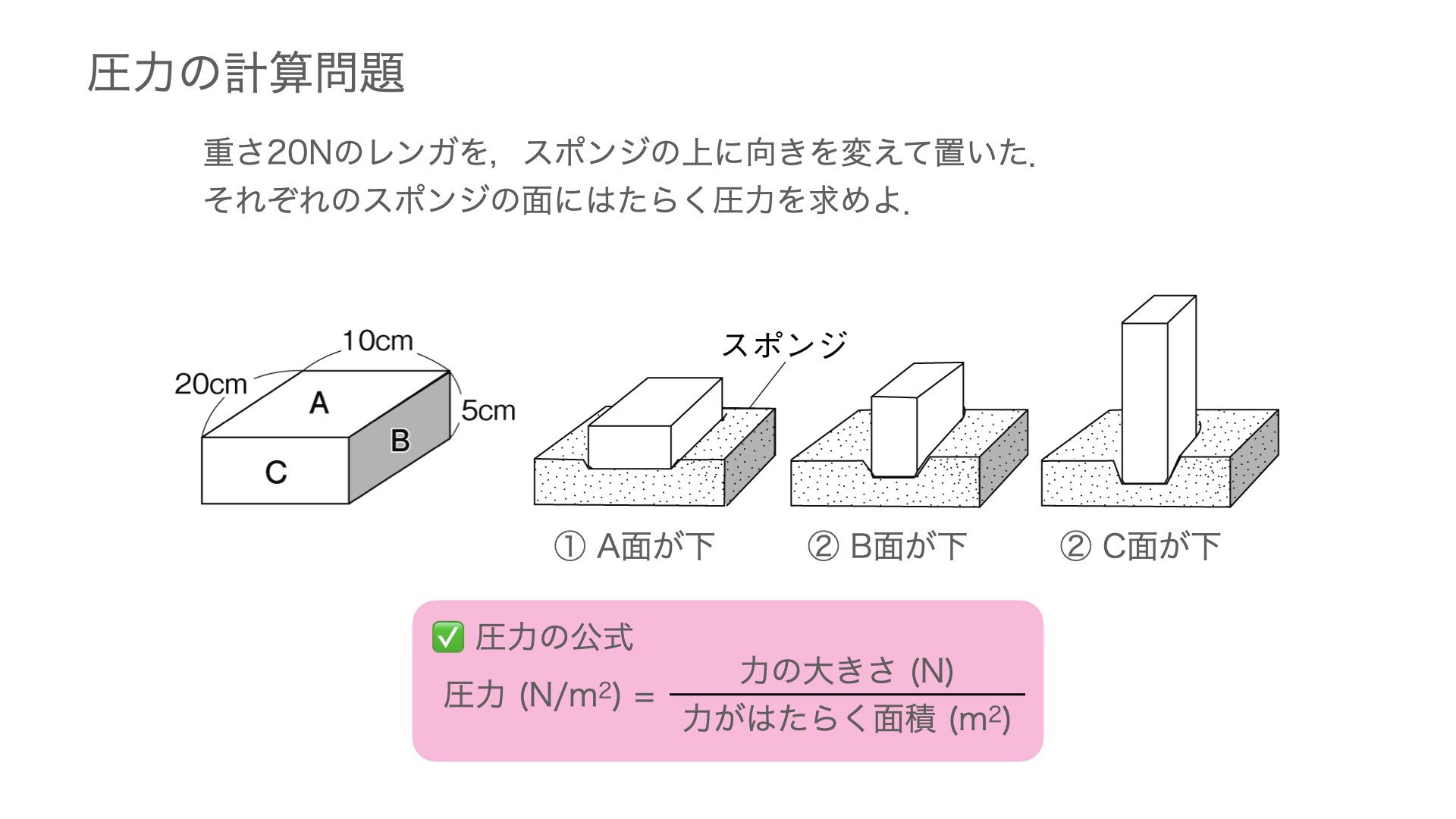


圧力の公式を覚えるコツと計算問題の解き方 理科デジノート


2
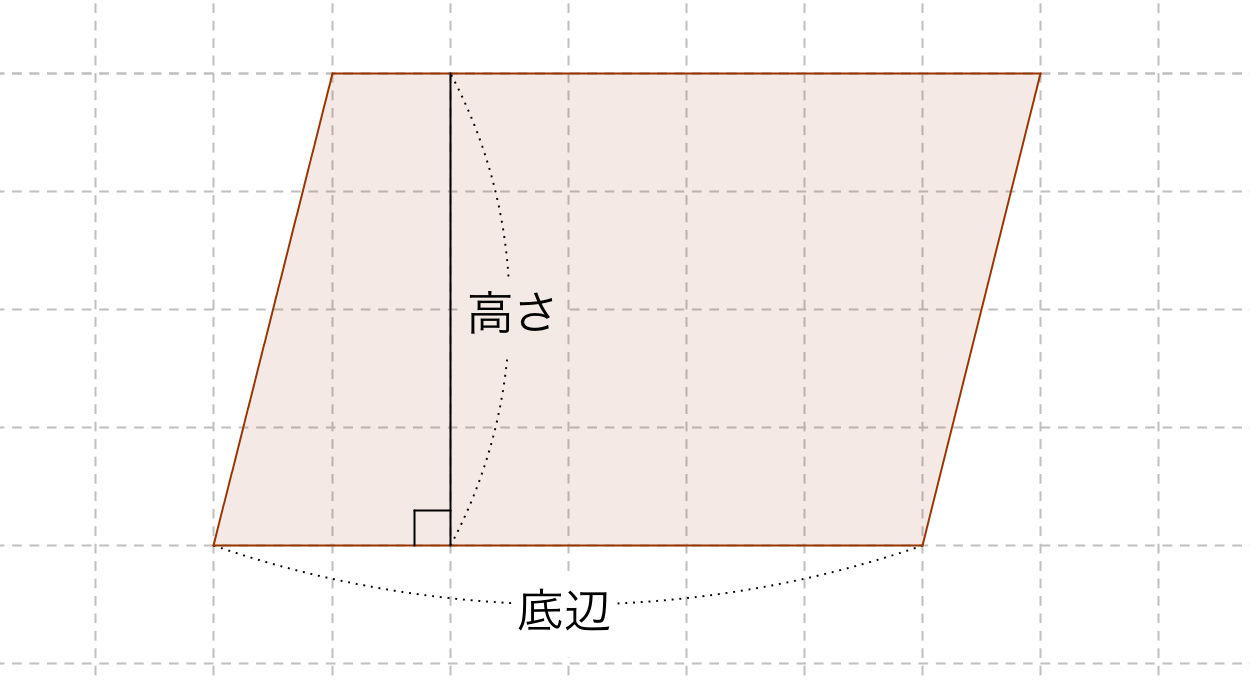


平行四辺形の面積の公式 算数の公式


Www Kyokyo U Ac Jp Kyoumu Jicci E Sansuu18 Pdf



どちゃ楽数学bot ブラーマグプタの公式 ブレードシュナイダーの公式で8 Pの場合 つまり円に内接する四角形の面積 Sを求める公式 検算用 T Co Lprfy7g2
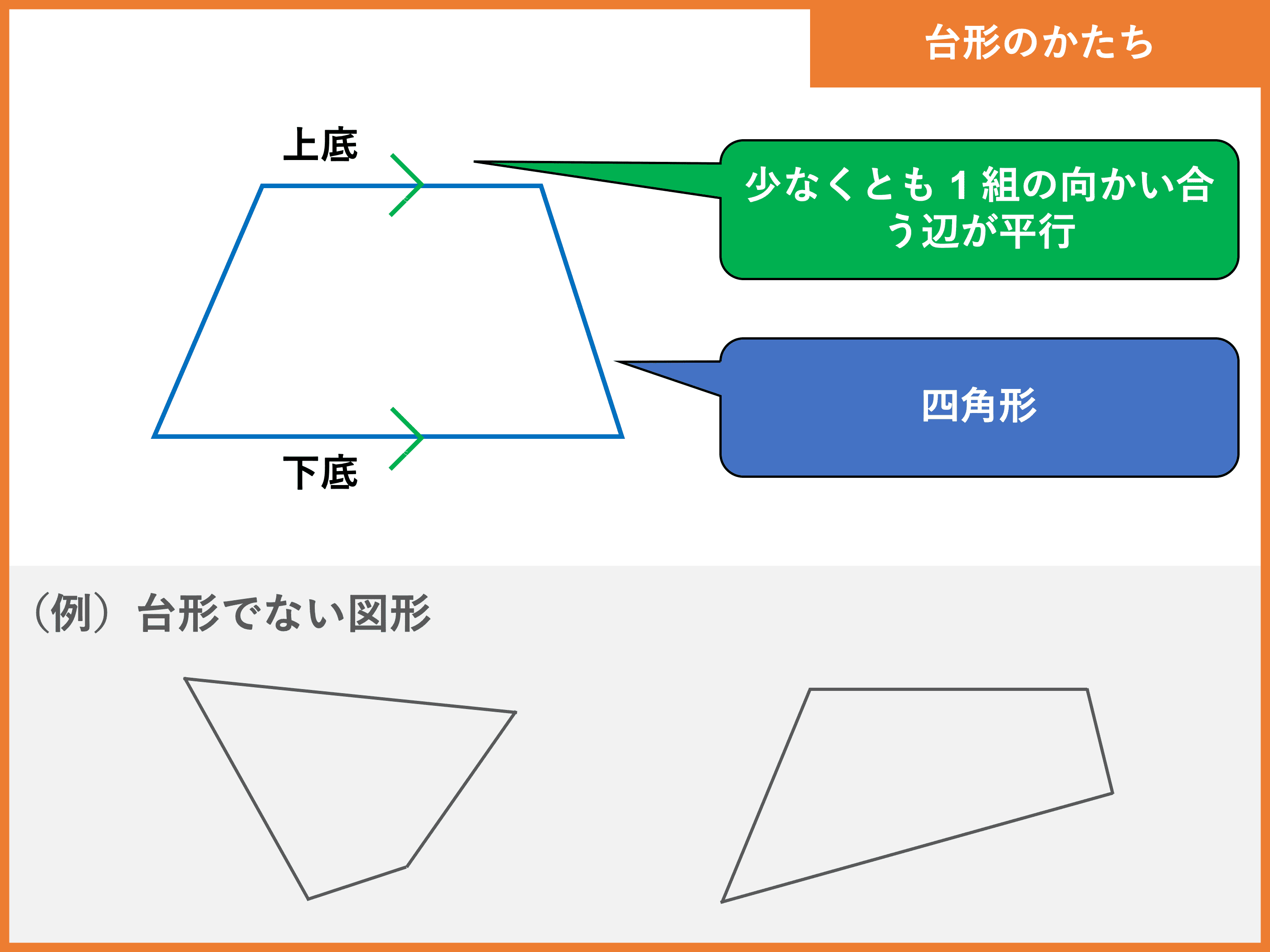


台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



円に内接する四角形の面積を四辺の長さで表す 2019年度前期日程の京都府立大学生命環境学部の入試 身勝手な主張


Http Www Ocec Ne Jp Shidoubu G Koujyou Zirei 56 035menseki Pdf



関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ



ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ


48s96ub7b0z5f Net Sankaku Menseki



高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月



簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく


2



余弦定理まとめ 公式 面積 問題と解き方 理系ラボ
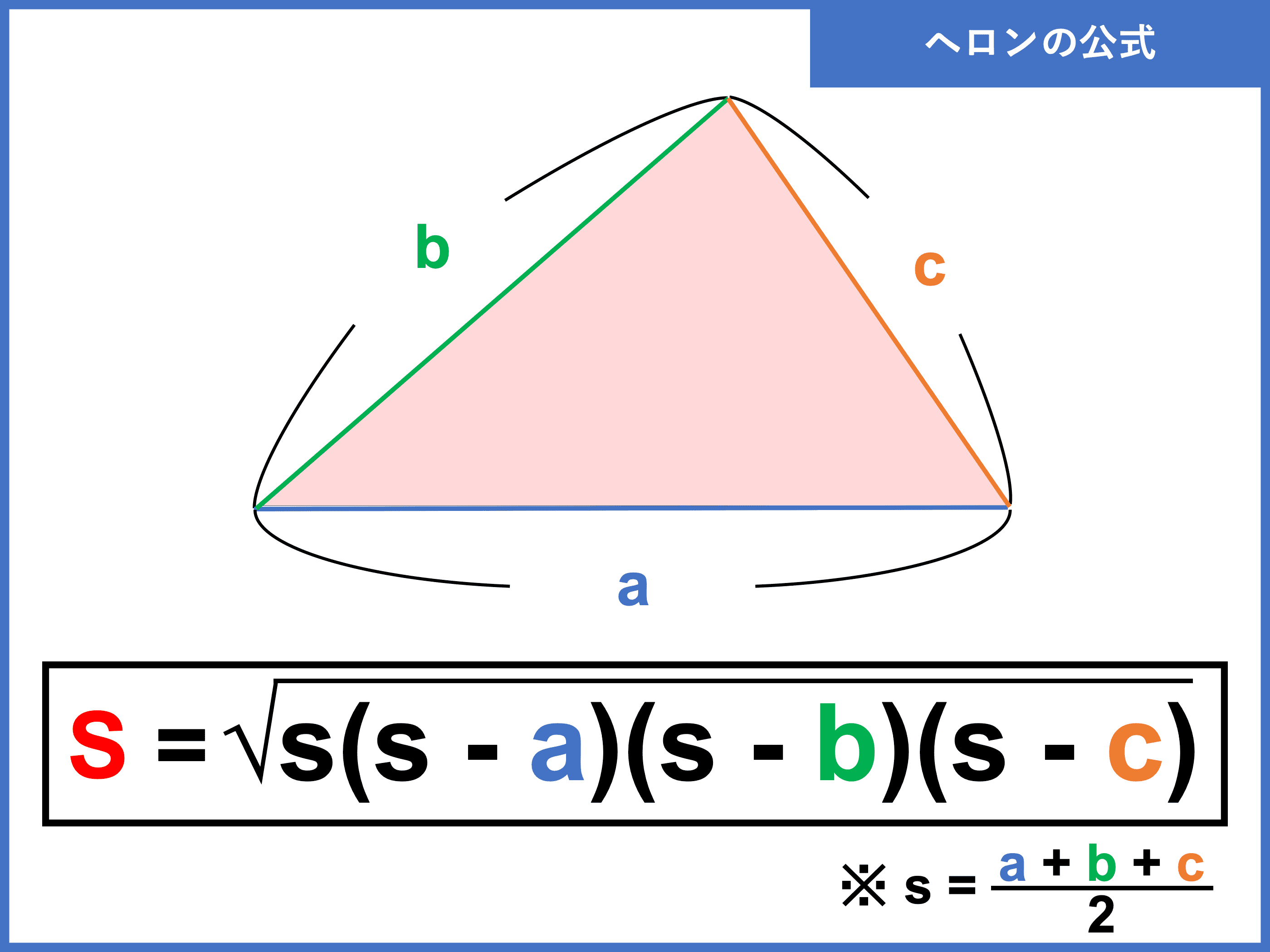


ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典


2


Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents S 048 Pdf


Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Elementaryschool Sansuu 5 509 Pdf



円の面積 練習応用 Youtube
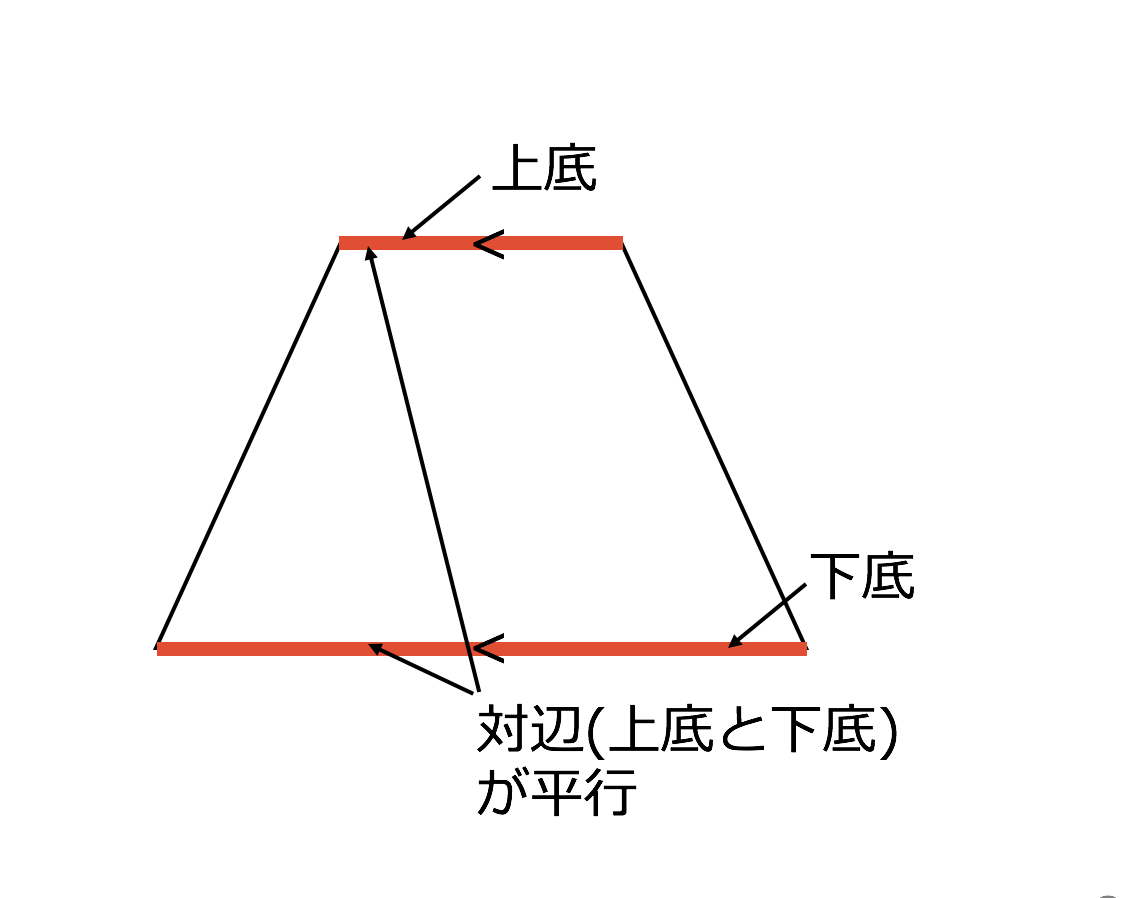


3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ


対角線から四角形の面積を求める公式を1分で証明する 怜悧玲瓏 高校数学を天空から俯瞰する



簡単公式 対角線で正方形の面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく


Www Souken Gakuin Com Cms Wp Content Uploads 04 F7173ba092cce010aadd Pdf



円に内接する四角形 小学5年への説明 再掲 Okwave


Http Www Magokoro Ed Jp Manage Contents Upload 5caaed1fefc Pdf



19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート


定積分で面積を求める 一歩一歩ぐんぐんブログ



高校数学 円に内接する四角形の面積ブラーマグプタの公式 裏技 の証明と円に内接しない四角形の面積ブレートシュナイダーの公式 裏技 受験の月


三角形 四角形の面積 Ict教材eboard イーボード



すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント



年の最高 図形 の 面積 無料の印刷物



拡大図 縮図の性質と問題の解き方 小学生に教えるための解説 数学fun
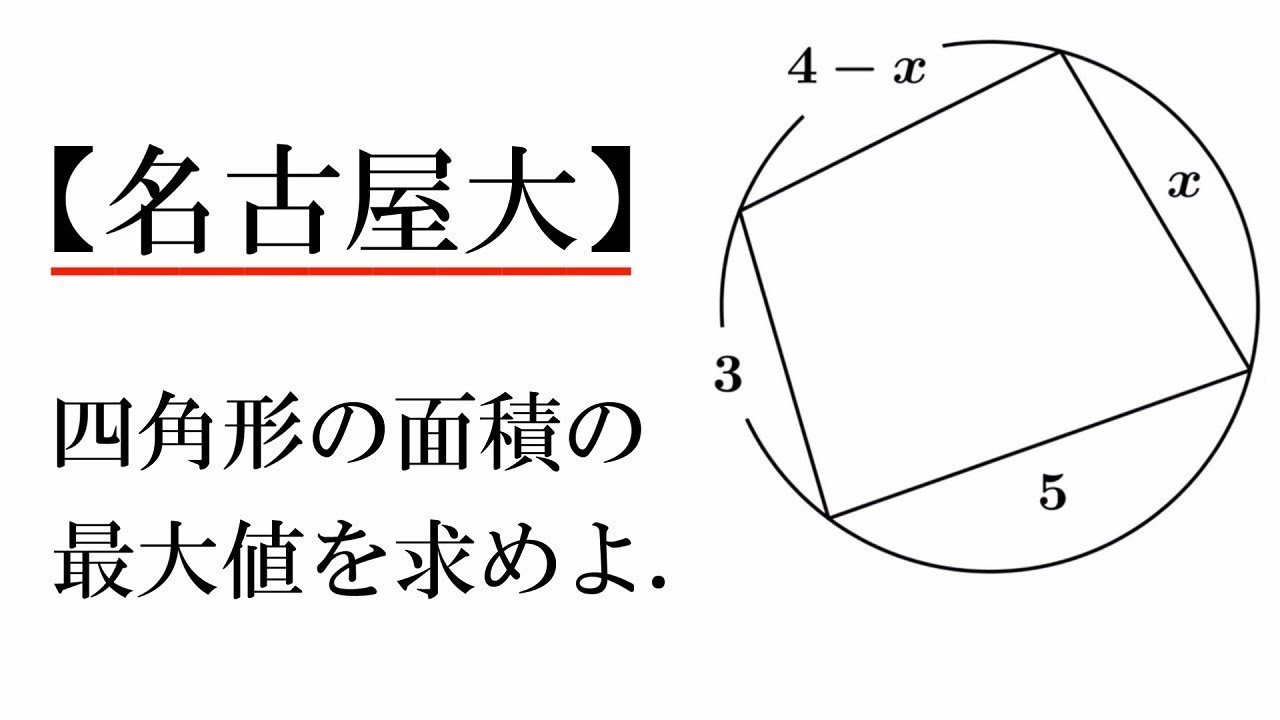


名古屋大 円に内接する四角形と三角比 超わかる 高校数学 A 演習 三角比 26 Youtube



拡大図 縮図の性質と問題の解き方 小学生に教えるための解説 数学fun
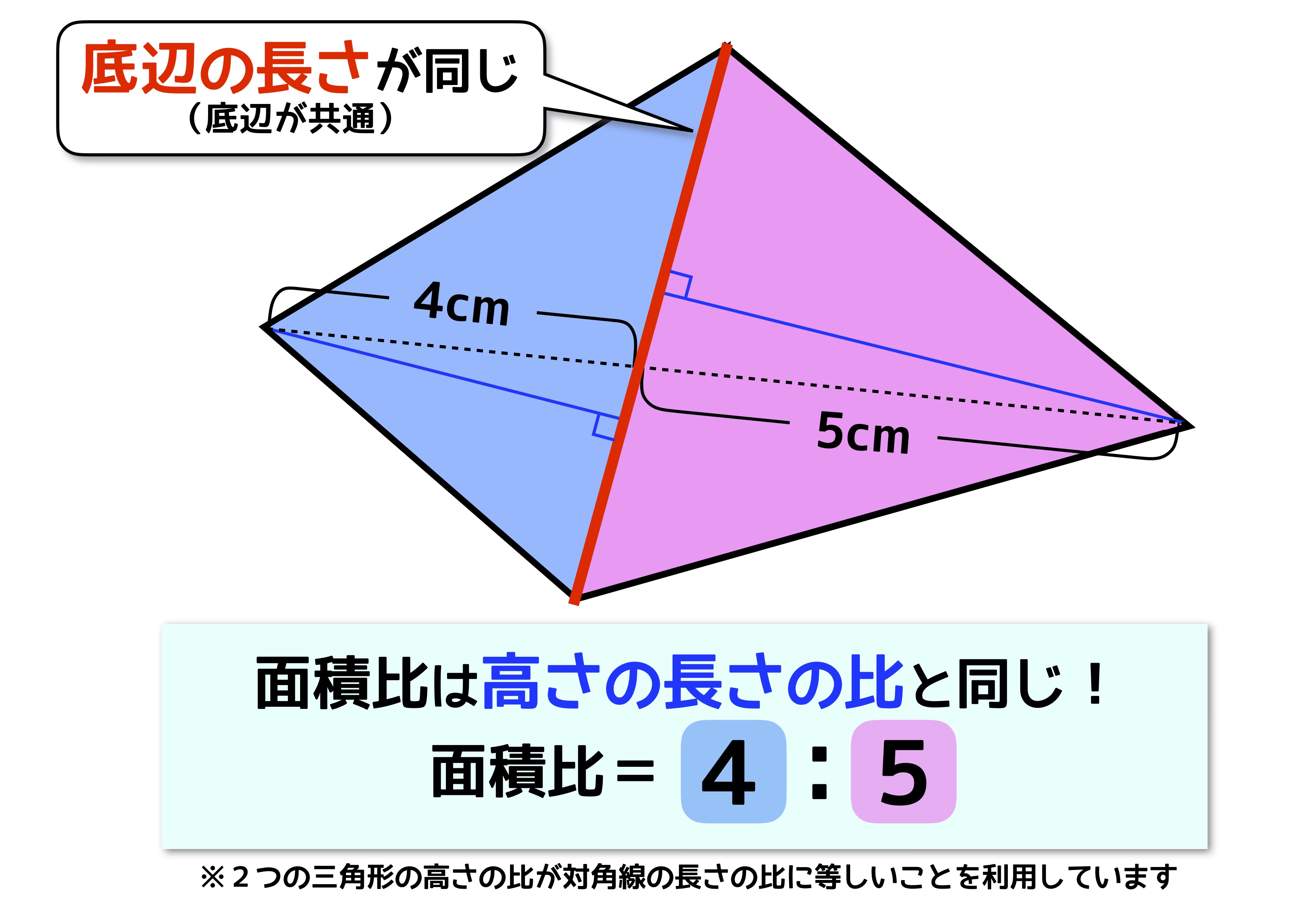


中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



小5 台形 面積の求め方 日本語版 Youtube



四角形の面積を2等分する直線の式の求め方 Okwave
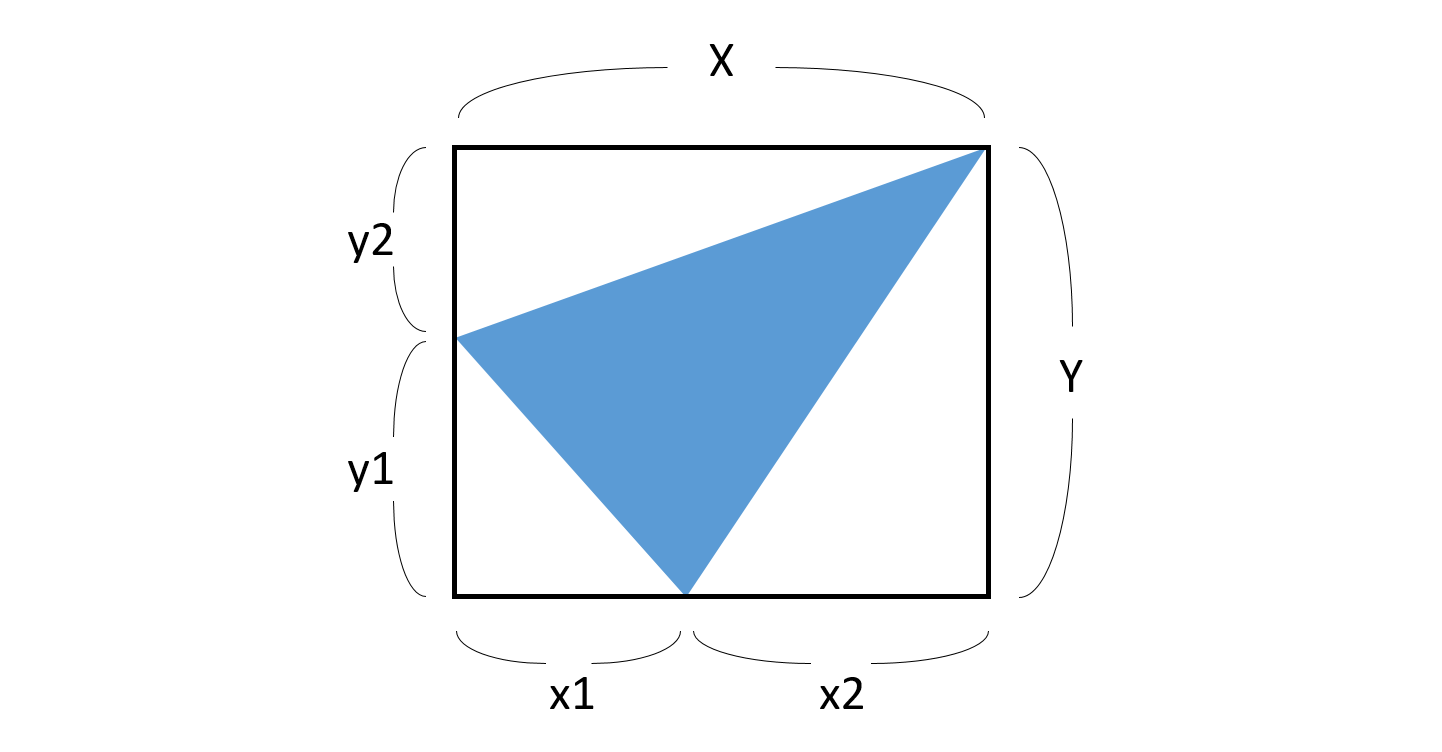


正方形の中にある三角形の面積の平均の求め方 三角形を分解して組み立てなおす Musyokutoumei



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典


平面図形と比 平行四辺形の面積比 新河岸 川越 の学習塾next Stage 自分に負けるな



小学校5年 算数 四角形の内角の和 Youtube
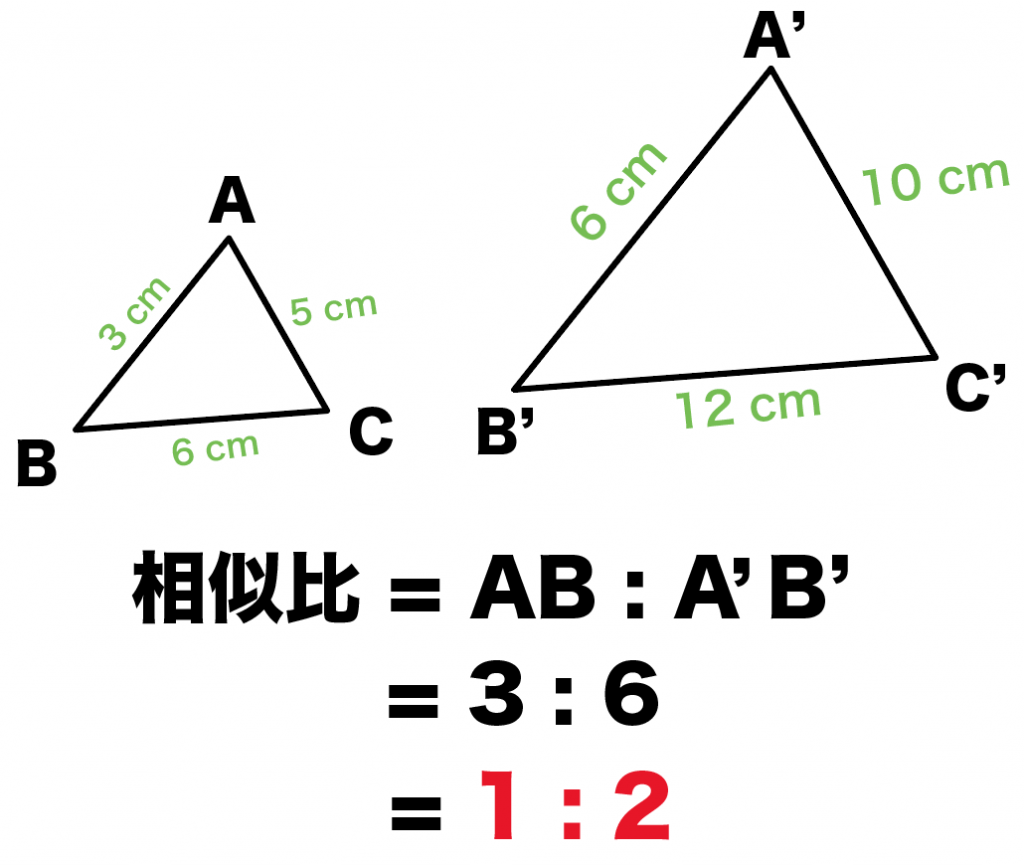


3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく


Http Www Saitama City Ed Jp Kyoukaken Pdf 22 Sansu Sansu Si Pdf
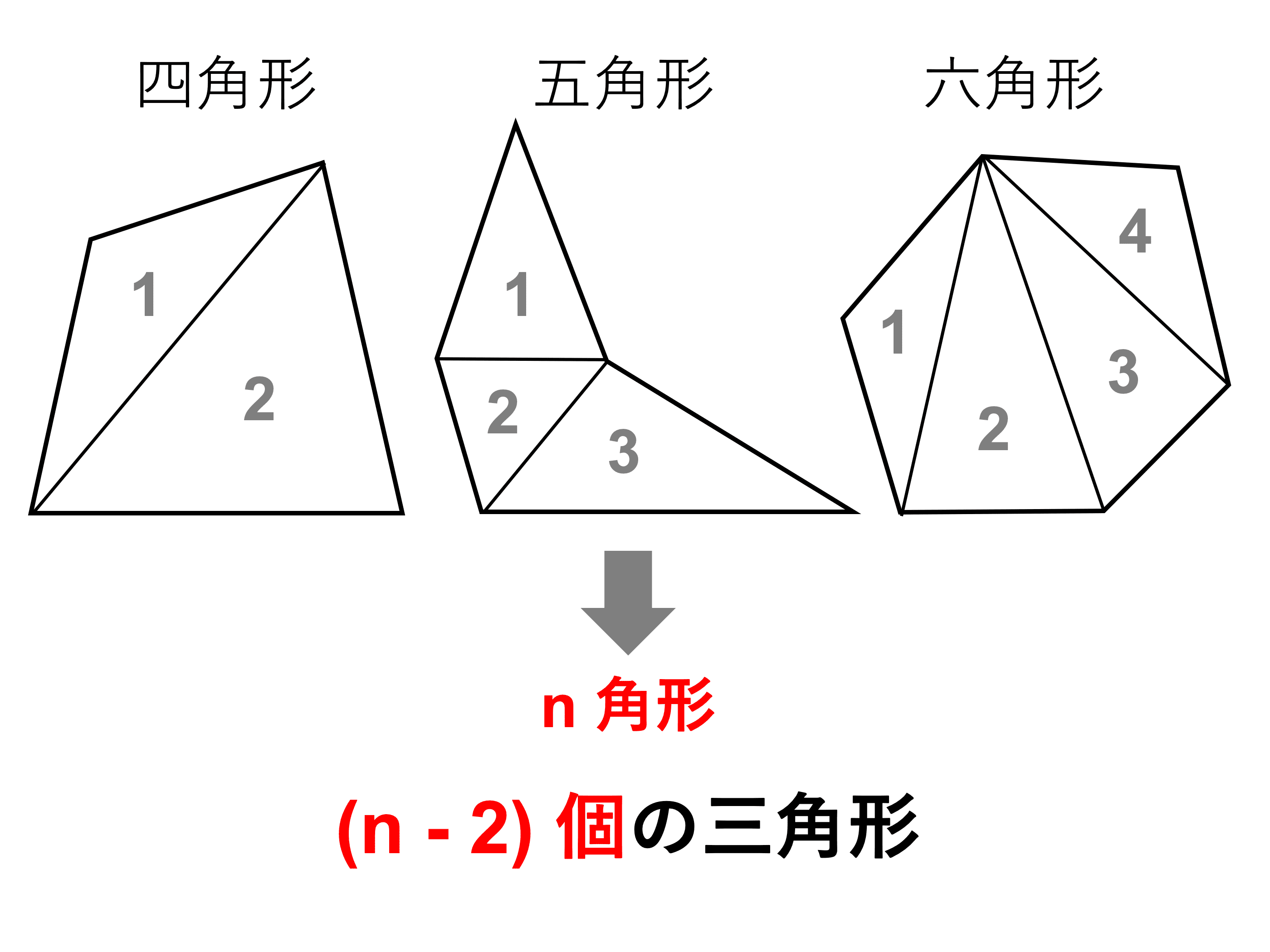


多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典


Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S5 004 Pdf
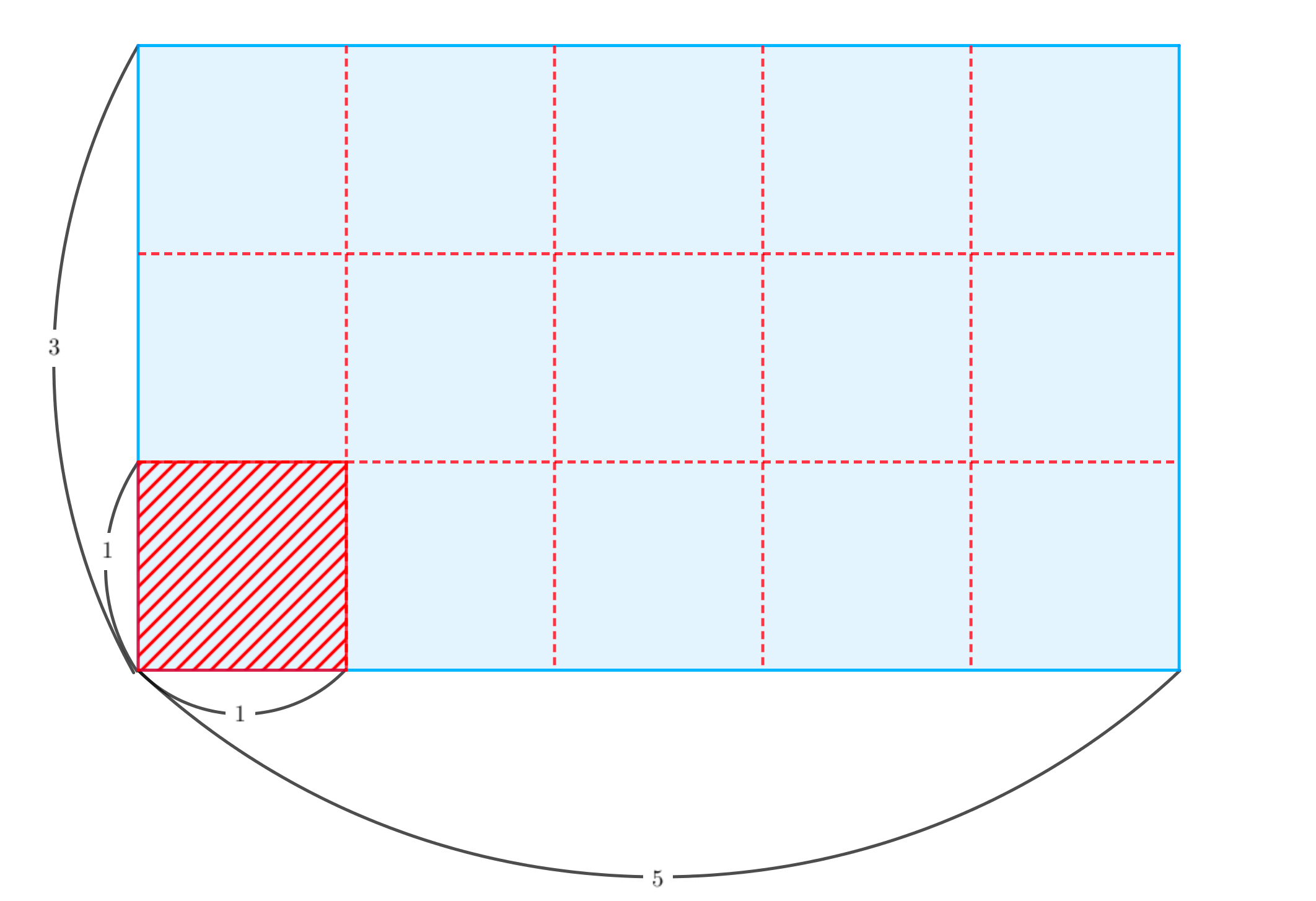


区分求積法 なぜ定積分は面積を表すの 文理どっちでも理解できるよう優しく解説 青春マスマティック



0 件のコメント:
コメントを投稿